Autonomous Area Search and Localization
This project tackled the problem of simultaneous localization and mapping (SLAM) using a TurtleBot 3 in a 4’ by 8’ obstacled arena.
To successfully complete this project, we implemented high-level algorithms including A* for path planning, pure pursuit for path following, and frontier detection for picking explorative goals.
We used ROS to manage and offload the multi-threaded computations necessary for the project.
Our implementation allowed us to accomplish the two phases of the project:
1.) Successfully map the entire arena and return to starting point
2.) Localize in the map and return to the starting point of the mapping (aka, the “kidnapped robot problem”)
TurtleBot mapping the arena.
Phase 1 Overview
We used the pre-existing ROS gmapping node to filter raw LIDAR readings and pose data into a map of the robot’s estimate of its location in its surrounding.
From this map data, frontiers were calculated by treating the map as an image consisting of known, unknown and occupied space. This allowed us to take advantage of fast, reliable image-processing techniques like binary dilation and contour detection from the OpenCV library to calculate the location of frontiers.
The frontiers were organized using a priority queue implementation over python’s built-in heapq algorithm. Frontiers were stored as a data structure with both the location of the frontier and its priority. The priority of a frontier was a linear combination of its size and cost to reach it (determined by A*). This allowed us to tune the weighting of the size and cost to have the robot continue down the “hallways” of the map without turning around and exploring a new area.
As the path following node controls the robot and drives it around the map, the gmapping node constantly updates the map and robot’s pose in it. Each node updates the next after finishing its calculations.
In the path planning and path following implementations we added extra functionality to ensure reliable, fast operations.
While using A* for path planning we recognized that the most optimal path was not the shortest, as we had implemented in previous labs and lectures, but the path the furthest from the walls.
To apply this to our path planning we added the distance to the center to our path cost. We used a breadth-first search through each map point, starting from the walls, to calculate the distance from the wall at each point. Then, the distance was inverted and normalized. This allowed for the path generation to be in the center of the “hallways” of the map, greatly reducing the chance of collisions with walls. Collisions were what we focused on minimizing in our approach to this project. Not only do collisions remove points from our final project score, they also undermine the reliability of the filtering done by gmapping, which can ruin the mapping portion (phase 1) of the project.
The robot path plans to stay in the center of the arena to prevent collisions with the wall. Collisions impact the reliaiblity of the filtering done in gmapping as the control inputs no longer align with robot’s movement.
We chose to implement pure pursuit to smoothly and reliably follow the paths generated by A*.
We modified the base pure pursuit algorithm to use proportional controllers for the angular and linear velocities of the robot.
We used a proportional controller for the angular velocity to control the rate at which the robot returns to the path independently from how far ahead the robot follows in the path. We took advantage of this to increase the rate at which the robot adjusts back to the path while still keeping a properly tuned “look ahead distance” that allowed for smooth path following.
We used a proportional controller for the linear velocity of the robot with the linear speed being proportional to the angular error. This allowed us to traverse through the arena at a relatively fast speed and earn a bonus as our team’s robot fully mapped the arena and returned home (phase 1 and 2 above) second fastest of all teams.
Controlling the linear velocity proportionally to the angular error allowed the robot to go fast when on a straight path and go slow when on a turn. Most importantly, this allowed the proportional coefficient for the angular velocity controller to be low, reducing oscillations while still maintaining an overall quick map traversal.
When using a proportional controller (right), the robot can stay tighter to the desired path than when traversing the arc tangent to the robot’s current heading and connected to the path (left). Photo.
Phase 2 Overview
After mapping was completed (phase 1), we used Monte Carlo localization implemented in the AMCL ROS package to localize our robot for phase 2 of the project. We successfully tackled the “kidnapped robot” problem of localizing in a known map. After this, we waited for user input for a goal destination in the map and traveled there using the localization provided by the AMCL node.
To localize in the map, the robot spun in place until the X and Y covariance was small enough for us to be certain of where the robot is in the map. The covariances, accessible from the AMCL node, provide insight into how certain the localization is of the robot’s pose in the map. Spinning in place allows for a control input (in this case an angular velocity) to be used by the algorithm to compare expected sensor readings with actual sensor readings and therefore for the robot’s pose to converge into a small area in the map. Once this area is small enough (gauged by the X and Y position covariances), the robot is then sure of its pose in the map to the extent necessary for the size of the field.
The path planning and path following were executed by the robot using the same implementations used in phase 1.
Initially, the robot had a lot of trouble path following in the final part of phase 2. The robot would osciallate around the path generated by A* and not be able to traverse the map without collisions.
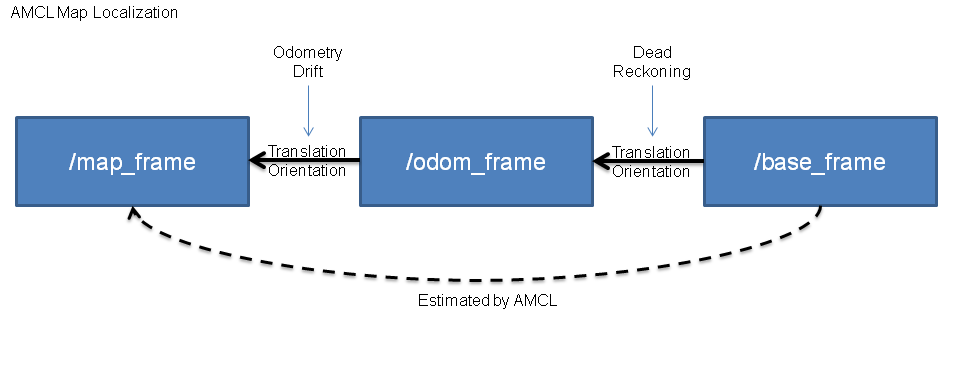
We tried tuning the pure-pursuit path following parameters before realizing the issue was much more fundamental. The AMCL node offers two ways to access its estimate of the robot’s pose: by publishing the localization updates to a topic, and by updating the transform of the robot’s pose in the map. Initially, we were only using the localization updates of the robot’s pose. This meant that we were completely ignoring the odometry updates from the robot while path following. This explained the jerky, oscillating movement of the robot as it tried to follow the path.
The AMCL node requires the robot’s odometry data to localize in the map. These localization updates take time to process and are published at a rate of about 1Hz. This means that inbetween the updates, the robot is essentially driving blind. This update rate was not fast enough to allow for correct path following.
We instead switched to the second way in which AMCL updates the robot’s pose: by using the transform updated by the AMCL node. This transform represents the robot’s pose in the map and is also updated by the robot’s odometry data. This update rate is much higher than when just using the AMCL localization updates (>200Hz) and allows for the odometry to be used in between the updates. As the robot’s pose is corrected by the localization odometry drift no longer is an issue. By tuning the rate at which the robot’s pose is updated with localization these two data streams (odometry and localization) were filtered together to allow for smooth pose estimation and successful path following.
The AMCL node updates the transform between the “map_frame” (map) and the “base_frame” (robot) alongside the odometry data from the robot. Photo.